1、引言
图像是人类最主要的信息源。在信息爆炸的时代,图像数据压缩技术是解决海量图像数据的存储和传输重要手段。因此寻求最佳的图像数据压缩技术也始终是信息技术领域中的一个研究热点。
随着医学成像技术和计算机技术的发展,数字化医学图像在医学临床诊断和教学研究中的应用日益广泛。一方面,从X射线、计算机断层扫描(CT)到核磁共振(MRI)、超声图像等的出现和发展,使得医学影像的质量越来越高,在医学诊断中扮演越来越重要的角色;另一方面,医学影像具有的信息量也越来越大,在医院使用PACS系统和远程医疗诊断系统中,均需大量的存储空间来存储和传输,图像数据的大小将会直接影响到传输的速度,导致目的地临床医生无法进行有效的诊断。医学图像压缩编码现已成为医疗信息学一个重要的研究方向,它要求重构图像不能有明显的失真,可以满足日益庞大的医学图像数据的压缩和传输任务。
2、空间域图像压缩算法介绍
2.1 频率域图像压缩算法的缺陷
近年来,图像数据的压缩取得了很大的发展,涌现了很多非常优秀的压缩算法。目前受到广泛应用,并已纳入新的国际标准的基于小波的压缩方法是一种成熟的、具有高保真压缩效果的压缩方法,但针对医学图像的压缩,该方法有一些严重的缺陷:
(1)基于小波的压缩方法是通过牺牲高频信息、保存低频信息的方法来换取压缩比的,图像经小波分解量化后会损失高频信息,并且随着压缩倍率的提高,高频信息的损失将越严重,这样会直接造成图像中纹理细节的损失;
(2)该方法必须以大面积图像为基础(随着小波分解所用基础面积的减小,恢复图像质量将急剧降低),并在多次二维小波分解基础上再做无失真编码后,才能得到高保真的压缩效果,但这种以大面积作为处理基础的算法是难于实现实时压缩的。
2.2 空间域图像压缩算法简介
正因为变换域编码存在以上缺陷,因此,人们又把目光投向了基于空间域的压缩方法。
在文献[4]中作者提出了多分辨率空间重采样图像压缩算法RBC算法。RBC算法在压缩比为4倍左右的应用情况下,其压缩质量不低于基于小波的压缩算法。但是因为RBC算法在对图像的结构描述上过于简单,随着压缩比的上升,其压缩质量迅速下降,因此,文献[5]在此基础上进行了改进,提出了基于模式特征的图像压缩算法SDBC算法。该算法以4×4的像素块作为基本的图像子区,用作压缩处理的基本单元,每个图像子区根据其纹理结构的复杂程度,分为平坦区、粗纹理区和细纹理区三类,以子区内图像的平均方差作为分类的准则,其压缩质量较RBC算法有显著提高。
虽然SDBC算法考虑了图像中纹理的分布,进行分区压缩,但是该算法只是用了4×4大小的块,并且只进行了三种分类模式,显然,这种方法并不能覆盖图像中的所有纹理。因此,本文延续SDBC的算法思想,借鉴H.264视频编码标准中的帧内编码技术,提出了基于空间预测和变换的压缩方法来解决以上的问题。
3、基于空间预测与变换的医学图像压缩方法
3.1 基于空间预测与变换的医学图像压缩方法概述
基于空域的图像压缩算法一般不能像基于小波变换的算法那样能进行全图的运算,而是要分块处理,为了便于计算机处理,一般图像的分块大小为2n×2n。本文选取4×4和16×16两种大小不同的块作为处理的窗口,以SAD作为窗口大小的选择的准则。本算法以16×16的宏块为单位进行编码。
基于空间预测和变换的医学图像压缩方法的大体流程如下:
(1) 把图像分成若干个16×16大小的宏块;
(2) 预测分析:对一个16×16的窗口进行预测分析。经过分析,得到最终进行编码的窗口大小:16×16或者4×4,以及最佳预测模式;
(3) 预测编码:根据(2)得到的窗口大小及最佳预测模式对该块进行变换、量化和扫描处理,此外,还要进行反变换和反量化,生成重建窗口。
(4) 对(3)中得到的数据进行熵编码;
(5) 重复(2)、(3)、(4),遍历图像中所有的16×16宏块。
3.2 预测类型
根据窗口的大小不同,本算法有两种预测类型,分别为4×4预测类型和16×16预测类型。图1中给出了产生4×4预测类型的像素分布,图2中给出了除模式2外的其他8种预测模式,而模式2是均值预测模式,它是用当前块的上边及左边像素的灰度值的均值来作为当前块每个像素的预测值。16×16预测类型有4种预测模式,分别为垂直预测方式、水平预测方式、直流预测方式和平面预测方式(如图3所示)。4×4预测类型适合预测细节多、变换相对较大、包含多个不同对象的图像区域,而16×16预测类型较适合于预测平滑的图像区域,对图像中相对不变的部分进行编码。
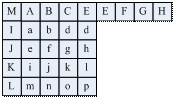
图1 4×4块预测类型的像素点分布

图2 4×4块预测方向

图3 16×16块预测模式
该算法在选择编码窗口时以绝对误差和SAD(Sum of Absolute Difference)作为判断准则。绝对误差和是指当前待编码块与预测块之间的差值绝对值之和,即残差之和。假设当前块用S(i,j)表示,预测值为pred(i,j),i,j=0,1,...,N,则
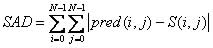
SAD值越小,说明图像的残差值越小,从而说明当前待编码块与预测块越接近,相应预测模式的预测的精度越高;反之,SAD值越大,说明图像的残差值越大,从而预测块不能很好的反应当前待编码块,相应预测模式的预测精度越低。
为了综合考虑各种预测模式的不同偏重方向性,当对宏块进行编码时会遍历所有的预测模式,并借助模式判决准则从中选出最优的模式作为最终的编码模式。
3.3 变换
由于离散余弦变换(DCT)非常近似于统计最佳的K-L变换,所以DCT通常被用于图像块的变换编码中。但是DCT有一个缺点:在DCT变换矩阵中的部分系数是无理数,在计算机上用迭代方法进行变换和反变换后,不能得到一致的初始值。本文采用H.264帧内编码的思想,用整数DCT[6]代替浮点数DCT。整数DCT对图像信号作用后可以获得与DCT类似的频率分解;同时,正交变换的目的是减少变换系数的相关性,使得变换系数的能量集中在较少的几个分量上,变换前后的能量并没有损失,在去除空间相关性上,整数DCT与DCT具有相同的效果。
本文中采用了两种变换:整数4×4 DCT和4×4的Hadamard变换。
整数4×4DCT变换减少了舍入误差,降低了计算复杂度,提高了运算精度;使用4×4块进行变换,使用于变换的块的尺寸缩小,能够减少块效应;同时,为了使小尺寸的变换方式对图像中较大面积的平滑区域不产生块之间的灰度差异,进一步降低DC系数间的相关性,对16个4×4块的DC系数进行第二次块变换,即Hadamard变换。
4、试验分析及结论
4.1 压缩性能比较
针对CT图像和MRI图像进行压缩(CT图像和MRI图像分别如图4、图5所示),用本文提供的算法的压缩结果与和JPEG2000压缩算法的压缩结果进行了对比,采用的客观评价指标为峰值信噪比(PSNR),结果见图6和图7(为了描述方便,本文提供的算法我们暂且用NEW来表示)。
为了比较两种算法的优劣,用下面的表格1表示用于测试图像的格式、大小和比特深度。
表1 用作比较的三种图像属性
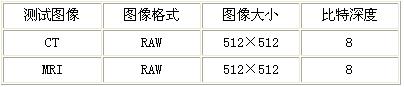

图4 CT图像

图5 MRI图像
客观评价参数峰值信噪比(PSNR)的定义如下:
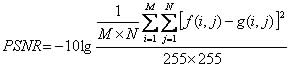
其中:f(i,j)为原始图像,g(i,j)为恢复图像,M×N为图像的宽×高

图6 CT图像的峰值信噪比曲线比较

图7 MRI图像的峰值信噪比曲线比较









